
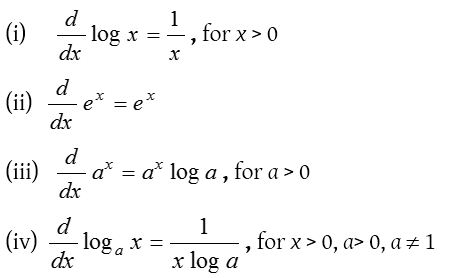
Differentiate both sides of this equation. Apply the natural logarithm to both sides of this equation getting. Look at some of the basic ways we can manipulate logarithmic functions: SOLUTION 3 : Because a variable is raised to a variable power in this function, the ordinary rules of differentiation DO NOT APPLY The function must first be revised before a derivative can be taken. This means that there is a “duality” to the properties of logarithmic and exponential functions. Take a moment to look over that and make sure you understand how the log and exponential functions are opposites of each other. In general, the logarithm to base b, written \(\log_b x\), is the inverse of the function \(f(x)=b^x\).

Therefore, the natural logarithm of x is defined as the inverse of the natural exponential function: For example log base 10 of 100 is 2, because 10 to the second power is 100. When we take the logarithm of a number, the answer is the exponent required to raise the base of the logarithm (often 10 or e) to the original number. Remember that a logarithm is the inverse of an exponential. We'll see one reason why this constant is important later on. The natural exponential function is defined as Review of Logarithms and Exponentialsįirst, let's clarify what we mean by the natural logarithm and natural exponential function. While there are whole families of logarithmic and exponential functions, there are two in particular that are very special: the natural logarithm and natural exponential function.
#Derivative of log a how to#
In this lesson, we'll see how to differentiate logarithmic and exponential functions. Differentiating a Logarithm or Exponentialīy now, you've seen how to differentiate simple polynomial functions, and perhaps a few other special functions (like trigonometric functions).


 0 kommentar(er)
0 kommentar(er)
